巴拿赫空间（Banach space）理论起源于一位波兰数学家斯特凡·巴拿赫（Stefan Banach）的早期研究工作。在他的博士论文中，巴拿赫首次完整地定义了这一类空间，并由此开启了一个全新的数学领域，称为泛函分析（functional analysis）。

说巴拿赫的职业道路“非同寻常”，都还算轻描淡写了。他高中毕业后，得出一个结论：数学已无新东西可供发掘。于是他决定转而在大学学习工程学。

在完成学业几年之后，一次偶然的邂逅永远改变了他的命运。一天，巴拿赫与朋友坐在公园长椅上，讨论他们最近学到的一门数学分支——测度论（measure theory）。就在这时，著名数学家乌果·斯坦豪斯（Hugo Steinhaus）路过，恰好听见他们提到了“勒贝格测度”（Lebesgue measure）这个词。

出于好奇，斯坦豪斯立即上前搭话。他们很快成了朋友。仅仅几天之后，巴拿赫就解出了一个困扰斯坦豪斯多时的数学问题。

斯坦豪斯在他的回忆录中写道：“从那以后，我们定期会面，并决定一起创立一个数学社团。”

这时的巴拿赫已年逾二十中期，他意识到原来数学世界远非已被探索殆尽。在斯坦豪斯的指导下，他茁壮成长，完全过上了数学家的生活——而他当时甚至没有任何数学学位。

他最终获得博士学位，是在另一位教授把他发表的多篇论文钉成一本，哄骗他去进行论文答辩之后的事。

这部非传统博士论文中，一个影响深远的部分，是他定义了一类全新的数学空间。这些空间带来了某种“怪异”的几何结构：在这里，球体会变成立方体，圆圈会变成方形，π的值甚至等于4。

这一“怪异性”源自于在Banach空间中定义“长度”的多种方式。技术上说，就是我们可以用许多种方式来在一个Banach空间上定义范数（norm）。

这种关于“长度”的抽象概念，正是定义Banach空间的两个关键特征之一。

那么现在，我们就从这位在职业道路上“偏离常规”的数学家，转而关注他对于“范数”这一数学概念的精准定义。

为了建立一点直观理解，我们从平面上的两个点开始考虑。可以使用毕达哥拉斯定理（Pythagorean theorem）来计算这两个点之间的距离。

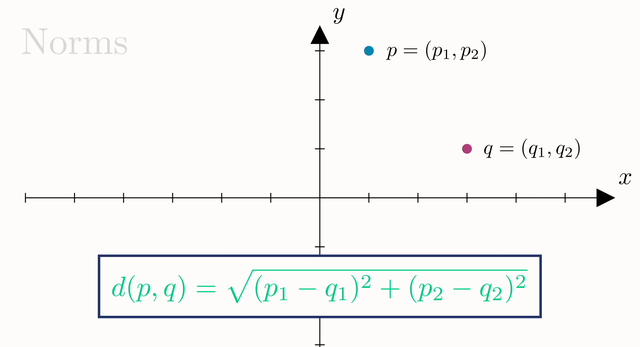
一般而言，我们可以用它的一个变形公式来计算平面上任意两点之间的距离。

也可以稍作改变，来得到一种略有不同的“距离”概念。

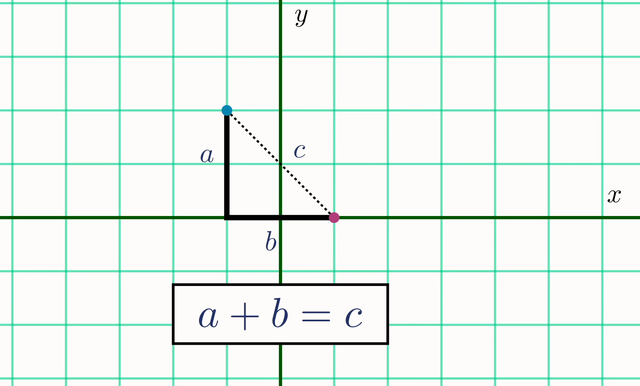
假设这个平面变成了一个网格状的结构，而且你不能走斜线，必须沿着网格线行走。这样一来，从一个点移动到另一个点，路径必须是沿着横线和竖线。

于是，两点之间的距离就变得简单了：不再是a^2 + b^2 = c^2，而是 a+b=c。

而对于任意两个点，这种“距离”的一般计算公式如下

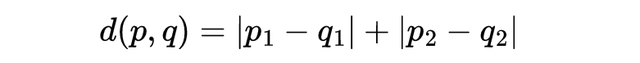
因为这种结构与纽约市著名的“曼哈顿街区网格”极为相似，这种几何被称为“曼哈顿几何”（Manhattan geometry），或者“出租车几何”（taxi cab geometry）。

而我们最开始提到的、基于勾股定理的标准距离定义，则被称为“欧几里得几何”（Euclidean geometry）。

出租车几何看起来人畜无害，但它却带来了几个非常违反直觉的结果。

回忆一下：一个圆的定义是由一组到圆心距离相等的点组成。

所以在欧几里得几何中，半径为2的圆，看起来就像我们平时所熟知的那个样子。

但在出租车几何中，如果我们仍然考虑所有到圆心“距离”为2的点，那么得到的形状却完全不同。

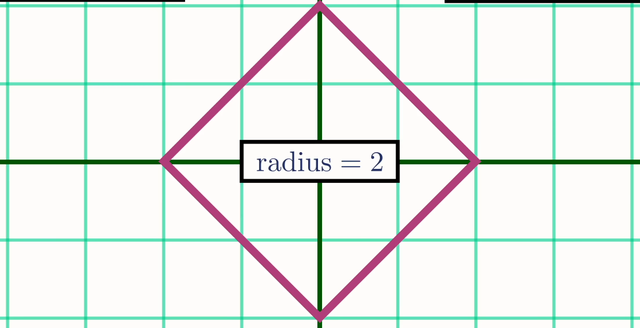
这个菱形，其实在出租车几何中，正是一个半径为2的“圆”。

更有趣的是，我们可以在这种几何中重新计算圆周率π的数值。

π的定义是圆的周长除以直径。在这个菱形中，每条边长为4，总周长为16，而直径为4。

所以，在出租车几何中，π的值等于4。

我们还可以再定义第三种距离概念，从而构建出另一种替代几何。

假设你仍然处于出租车几何的那种网格之中，但这一次，总距离的定义是：你在x方向和y方向分别走了多远，取这两者中的较大值。

而由这种定义所产生的几何结构，被称为契比雪夫几何（Chebyshev geometry），得名于俄国数学家帕夫努季·契比雪夫（Pafnuty Chebyshev）。

在这里，半径为2的圆，看起来就像我们通常所说的一个“正方形”，而π的值，再次是4。

那么，所有这些内容是如何与 Banach 空间和范数联系起来的呢？

事实上，以上这三种几何空间——欧几里得几何、出租车几何、契比雪夫几何——其实全都是 Banach 空间，每一个都有各自独特的范数定义。

虽然我们一直在谈论“两点之间的距离”这一概念，范数其实是距离的一种特殊情况。

距离通常是指两个点之间的“间隔”，而范数是指一个向量的“长度”——你可以把它看成是箭头从尾到头的距离。

而这不仅适用于我们直观中的“箭头”向量，还适用于一切抽象数学中的向量。

所以，就像我们在这三种几何中定义了三种不同的“距离”规则，我们同样可以有三种不同的方式来定义向量的“长度”。

它们都是数学上自洽的，并且都满足以下这几点条件——这也正是范数的严格定义：

任何在其上定义了一个范数的空间，就被称为“赋范空间”（normed space）。

在数学空间的层级结构中，我们可以从最抽象的起点开始：一个空间，只是一些抽象向量的集合，这种空间被称为“向量空间”（vector space）。

此时我们尚不能测量向量的长度，也无法定义它们之间的角度关系。

为了实现这些操作，我们可以在向量空间上定义一个“内积”（inner product）——本质上是一种推广的点积，它需满足一套特定条件，

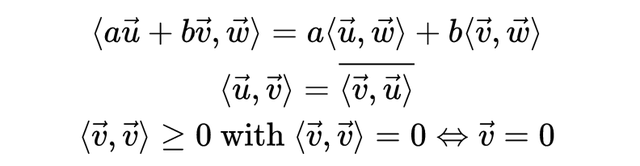
这时，向量空间就升级为“内积空间”（inner product space）。

如果我们仅仅只关心向量的长度，而不关心它们之间的夹角，那么我们可以在该空间上直接定义一个范数。

在许多情况下，一个向量的范数可以通过先计算它与自身的内积，再开平方得到。

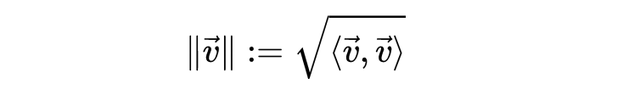
在这种情况下，范数就依赖于内积。技术术语称之为：该范数是“由内积诱导”的（induced by the inner product）。

不过，并非所有的范数都是这样定义的。有些范数与内积毫无关系。

事实上，有一个非常方便的定理指出：只有在满足所谓的“平行四边形法则”（parallelogram law）时，范数才一定由内积诱导。

因此，所有的内积空间都是赋范空间，但并非所有的赋范空间都是内积空间。

向量的“长度”只是“距离”的一种特殊定义方式。

更一般意义上的“距离”在数学中称为“度量”（metric），它是一个函数，满足如下条件：

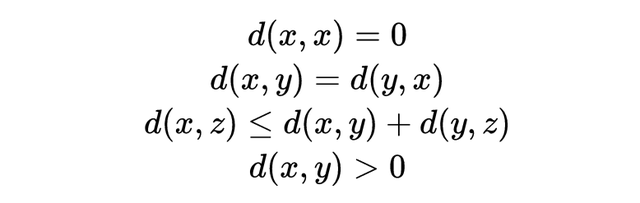
就像内积诱导范数，范数也可以诱导出度量。但并非所有的度量都来自于某个范数。

因此，在一个空间上定义一个度量，会带来一个更为广义的空间类别，即“度量空间”（metric space）。

这就构成了一个漂亮的数学空间层级结构：

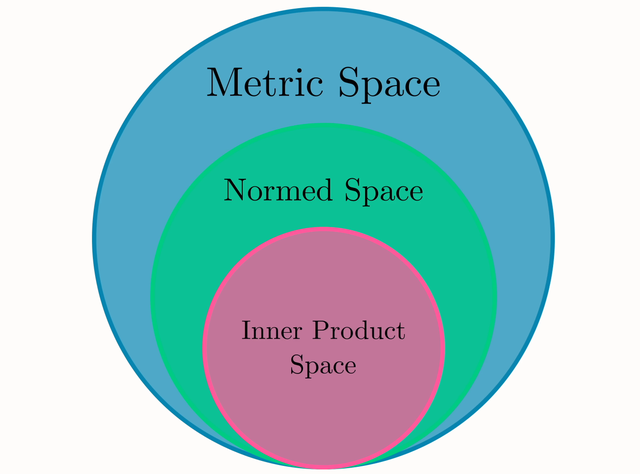
每一个内积空间都是赋范空间；

每一个赋范空间都是度量空间。

于是，Banach 空间就处于这个层级中的中间位置：它是一个“赋范空间”，再加上一个额外的条件。

这个条件就是：完备性（completeness）。

所谓一个空间是“完备”的，意思是：在这个空间中，所有收敛的序列的极限都还在这个空间内部。

更准确地说，如果一个柯西序列（Cauchy sequence）在某个空间里收敛到空间外的某个点，那么这个空间就是“不完备的”。

但如果你对这个空间进行扩充，使得每一个柯西序列最终都能收敛到空间内部某一点，那么这个扩充之后的空间，就是“完备”的。

在这个阶段，我们需要明确区分 Banach 空间和另一类重要的数学空间——希尔伯特空间（Hilbert space）。

Banach 空间是完备的赋范空间，而希尔伯特空间是完备的内积空间。

这意味着：希尔伯特空间是那种满足“平行四边形恒等式”的 Banach 空间。

所以每一个希尔伯特空间必定是一个 Banach 空间，但并不是每个 Banach 空间都是希尔伯特空间。

为了突出这种区别，我们接下来会研究一类与圆和球有关的 Banach 空间家族：L^p 空间。

所谓 L^p 空间，是指所有满足如下条件的数列所组成的空间：

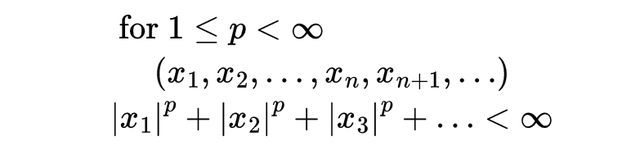
每一个具体的 p 值都会对应一个不同的空间。

当 p=1 时，L^1 是所有满足该级数和有限的数列所构成的空间,

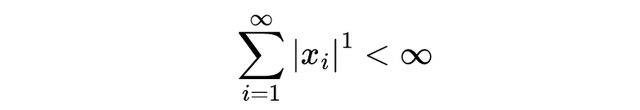
当 p=2 时，L^2 包含所有该级数和有限的数列，

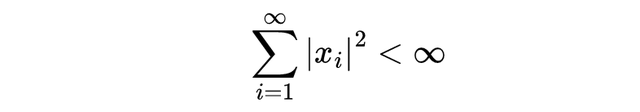
依此类推。

我们可以在所有这些 L^p 空间上定义如下形式的范数，使它们变成赋范空间：

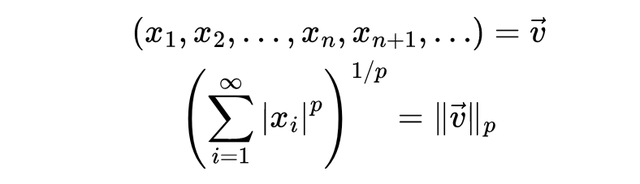
而且，这些空间都是完备的，因此它们全都是 Banach 空间。

不仅如此，我们还可以在每个 p 值下选定不同的 n 值，对应于向量的维度。

比如，在二维空间中：

当 p=1 时，我们得到L^1 范数。箭头的长度（即向量的范数）按以下方式计算：

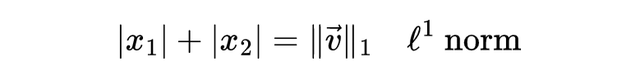
这就自然地引出了出租车几何。

当 p=2 时，我们得到 L^2 范数，即欧几里得范数，它对应的几何就是我们熟悉的欧几里得几何。

当 p→∞ 时，得到所谓的 L∞ 范数，也称为最大范数，它所对应的几何就是契比雪夫几何。

在继续探讨所有其他 p 值时，我们先来看看三维空间下的表现。

现在你可能会问：为什么我们只考虑了 p=1 到 无穷 那 p 介于 0 到 1 之间的情况呢？

还记得我们刚刚说的：度量空间比赋范空间更一般吗？

从 p=0 到 p=1 的这些数列仍然可以构成度量空间——我们可以定义某种距离概念。

但是在这些情况下，度量不再来源于任何一个范数。你无法在这些空间里定义出一个符合范数定义的函数。

然而，一旦 p=1，一切就变了。从这一点开始，所有这些度量都可以由范数诱导。但在所有这些无穷多种 Banach 空间中，只有一种范数是由内积诱导而来的：那就是当 p=2 时的 L^2 空间。也就是说，L^2 是这些 Banach 空间中唯一的希尔伯特空间。